Where the techniques of Maths
are explained in simple terms.
Calculus - Differentiation.
Ideas about concavity.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
The second derivative of a function - that is the derivative of the gradient function - provides information about the concavity of a curve.
As noted elsewhere, the shape of a curve where the curve has:
| positive concavity looks like: | 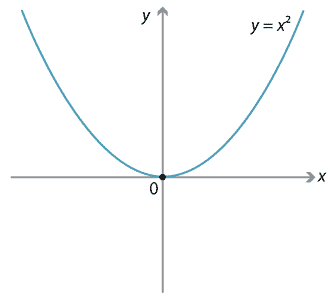 |
| negative concavity looks like: | 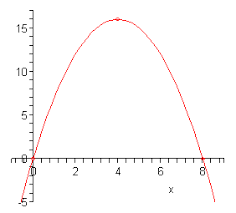 |
In questions asking for maximum or minimum values of a curve, we can usually just substitute the x values into the second derivative and show it has a positive or a negative concavity and interpret that.
If it is too difficult to obtain the second derivative, we need to show a change of gradient about the x value with a table and so not worry about obtaining the second derivative (i.e. the nature of the inflection).
A horizontal point of inflection has
- zero gradient (i.e. f '(x) = 0; AND
- zero concavity (i.e. f ''(x) = 0.
Here convention dictates that we have to prove/show that the sign of the curve's concavity changes about the point of zero concavity by using a table and substituting a value for x on each side of the value we obtained by solving the equation by assuming zero concavity. Examples are shown of these tables in the solutions to the questions.
Special interpretation of zero concavity.
When we determine the second derivative function (i.e. f "(x)) and put its equation equal to zero, then we are really looking for the stationary points of the first derivative. We have just moved down one layer BUT we are still doing the same thing (just with different equations).
HENCE - when the second derivative function (concavity) equals zero, the first derivative function (i.e. the gradient function) equals a maximum or a minimum. So if we need the steepest tangent for a curve:
- find the second derivative;
- put it = 0;
- find the x value;
- substitute that x value into the first derivative to find the steepest gradient (either positive or negative).